Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They appear in a number of contexts, for example they are closely related to the values of the Riemann zeta function at negative integers and appear in the Euler–Maclaurin formula. The values of the first few Bernoulli numbers are B0 = 1, B1 = −1/2, B2 = 1/6, B3 = 0, B4 = −1/30. (Some authors use B1 = +1/2 and some write Bn for B2n.)
The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jakob Bernoulli, after whom they are named, and independently by Japanese mathematician Seki Kōwa. Seki's discovery was posthumously published in 1712[1][2] in his work Katsuyo Sampo; Bernoulli's, also posthumously, in his Ars Conjectandi of 1713.
They appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.
In note G of Ada Lovelace's notes on the analytical engine from 1842, Lovelace describes an algorithm for generating Bernoulli numbers with Babbage's machine.[3] As a result, the Bernoulli numbers have the distinction of being the subject of the first computer program.
Sum of powers
Closed forms of the sum of powers for fixed values of m
are always polynomials in n of degree m + 1. Note that Sm(0) = 0 for all m ≥ 0 because in this case the sum is the empty sum. The coefficients of these polynomials are related to the Bernoulli numbers by Bernoulli's formula:
where B1 = +1/2.
Let n ≥ 0. Taking m to be 0 and B0 = 1 gives the natural numbers 0, 1, 2, 3, ... (sequence A001477 in OEIS).
Taking m to be 1 and B1 = 1/2 gives the triangular numbers 0, 1, 3, 6, ... (sequence A000217 in OEIS).
Taking m to be 2 and B2 = 1/6 gives the square pyramidal numbers 0, 1, 5, 14, ... (sequence A000330 in OEIS).
Some authors state Bernoulli's formula in a different way:
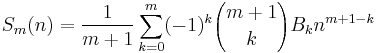 ,
,
where B1 = −1/2. In the next section consequences of the resulting differences will be commented on as they are likely to produce some confusion.
Bernoulli's formula is sometimes called Faulhaber's formula after Johann Faulhaber who also found remarkable ways to calculate sum of powers.
Faulhaber's formula was generalized by V. Guo and J. Zeng to a q-analog (Guo & Zeng 2005).
Definitions
Many characterizations of the Bernoulli numbers have been found in the last 300 years, and each could be used to introduce these numbers. Here only four of the most useful ones are mentioned:
- a recursive equation,
- an explicit formula,
- a generating function,
- an algorithmic description.
For the proof of the equivalence of the four approaches the reader is referred to mathematical expositions like (Ireland & Rosen 1990) or (Conway & Guy 1996).
Unfortunately in the literature the definition is given in two variants: Despite the fact that Bernoulli defined B1 = 1/2, some authors set B1 = −1/2 (more on different conventions below). In order to prevent potential confusions both variants will be described here, side by side.
Recursive definition
The recursive equation is best introduced in a slightly more general form
This equation defines rational numbers Bm(n) for all integers n ≥ 0, m ≥ 0. 00 has to be interpreted as 1. The recursion has its base in B0(n) = 1 for all n. The two variants now follow by setting n = 0 respectively n = 1. Additionally the notation is simplified by erasing the reference to the parameter n.
-
n = 0 n = 1 ![B_m = \left[ m = 0 \right] -\sum_{k=0}^{m-1}\binom mk\frac{B_k}{m-k%2B1}](/2012-wikipedia_en_all_nopic_01_2012/I/7408ca283a4766fa4a414b0e1c01be2d.png)
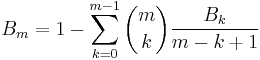
Here the expression [m = 0] has the value 1 if m = 0 and 0 otherwise (Iverson bracket). Whenever a confusion between the two kinds of definitions might arise it can be avoided by referring to the more general definition and by reintroducing the erased parameter: writing Bm(0) in the first case and Bm(1) in the second will unambiguously denote the value in question.
Explicit definition
Starting again with a slightly more general formula
the choices n = 0 and n = 1 lead to
-
n = 0 n = 1 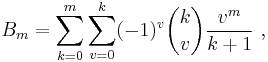
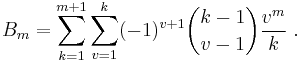
There is a widespread misinformation that no simple closed formulas for the Bernoulli numbers exist (Gould 1972). The last two equations show that this is not true. Moreover, already in 1893 Louis Saalschütz listed a total of 38 explicit formulas for the Bernoulli numbers (Saalschütz 1893), usually giving some reference in the older literature.
Generating function
The general formula for the generating function is
The choices n = 0 and n = 1 lead to
-
n = 0 n = 1 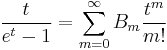
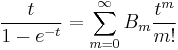
Algorithmic description
Although the above recursive formula can be used for computation it is mainly used to establish the connection with the sum of powers because it is computationally expensive. However, both simple and high-end algorithms for computing Bernoulli numbers exist. Pointers to high-end algorithms are given the next section. A simple one is given in pseudocode below.
Algorithm Akiyama–Tanigawa algorithm for Bn Input: Enter integer n. Output: Bn.
for m from 0 by 1 to n do
A[m] ← 1/(m+1)
for j from m by -1 to 1 do
A[j-1] ← j×(A[j-1] - A[j])
return A[0] (which is Bn)
- "←" is a loose shorthand for "changes to". For instance, "largest ← item" means that the value of largest changes to the value of item.
- "return" terminates the algorithm and outputs the value that follows.
Efficient computation of Bernoulli numbers
In some applications it is useful to be able to compute the Bernoulli numbers B0 through Bp − 3 modulo p, where p is a prime; for example to test whether Vandiver's conjecture holds for p, or even just to determine whether p is an irregular prime. It is not feasible to carry out such a computation using the above recursive formulae, since at least (a constant multiple of) p2 arithmetic operations would be required. Fortunately, faster methods have been developed (Buhler et al. 2001) which require only O(p (log p)2) operations (see big-O notation).
David Harvey (Harvey 2008) describes an algorithm for computing Bernoulli numbers by computing Bn modulo p for many small primes p, and then reconstructing Bn via the Chinese Remainder Theorem. Harvey writes that the asymptotic time complexity of this algorithm is O(n2 log(n)2+eps) and claims that this implementation is significantly faster than implementations based on other methods. Harvey's implementation is included in Sage since version 3.1. Using this implementation Harvey computed Bn for n = 108, which is a new record (October 2008). Prior to that Bernd Kellner (Kellner 2002) computed Bn to full precision for n = 106 in December 2002 and Oleksandr Pavlyk (Pavlyk 2008) for n = 107 with 'Mathematica' in April 2008.
-
Computer Year n Digits* J. Bernoulli ~1689 10 1 L. Euler 1748 30 8 J.C. Adams 1878 62 36 D.E. Knuth, T.J. Buckholtz 1967 1672 3330 G. Fee, S. Plouffe 1996 10000 27677 G. Fee, S. Plouffe 1996 100000 376755 B.C. Kellner 2002 1000000 4767529 O. Pavlyk 2008 10000000 57675260 D. Harvey 2008 100000000 676752569
- Digits is to be understood as the exponent of 10 when B(n) is written as a real in normalized scientific notation.
Different viewpoints and conventions
The Bernoulli numbers can be regarded from four main viewpoints:
- as standalone arithmetical objects,
- as combinatorial objects,
- as values of a sequence of certain polynomials,
- as values of the Riemann zeta function.
Each of these viewpoints leads to a set of more or less different conventions.
- Bernoulli numbers as standalone arithmetical objects.
Associated sequence: 1/6, −1/30, 1/42, −1/30,...
This is the viewpoint of Jakob Bernoulli. (See the cutout from his Ars Conjectandi, first edition, 1713). The Bernoulli numbers are understood as numbers, recursive in nature, invented to solve a certain arithmetical problem, the summation of powers, which is the paradigmatic application of the Bernoulli numbers. It is misleading to call this viewpoint 'archaic'. For example Jean-Pierre Serre uses it in his highly acclaimed book A Course in Arithmetic which is a standard textbook used at many universities today. - Bernoulli numbers as combinatorial objects.
Associated sequence: 1, +1/2, 1/6, 0,....
This view focuses on the connection between Stirling numbers and Bernoulli numbers and arises naturally in the calculus of finite differences. In its most general and compact form this connection is summarized by the definition of the Stirling polynomials σn(x), formula (6.52) in Concrete Mathematics by Graham, Knuth and Patashnik. - Bernoulli numbers as values of a sequence of certain polynomials.
Assuming the Bernoulli polynomials as already introduced the Bernoulli numbers can be defined in two different ways:
Bn = Bn(0). Associated sequence: 1, −1/2, 1/6, 0,....
Bn = Bn(1). Associated sequence: 1, +1/2, 1/6, 0,....
The two definitions differ only in the sign of B1. The choice Bn = Bn(0) is the convention used in the Handbook of Mathematical Functions. - Bernoulli numbers as values of the Riemann zeta function.
Associated sequence: 1, +1/2, 1/6, 0,.... This convention agrees with the convention Bn = Bn(1) (for example J. Neukirch and M. Kaneko). The sign '+' for B1 matches the representation of the Bernoulli numbers by the Riemann zeta function. In fact the identity nζ(1 − n) = (−1)n+1Bn valid for all n > 0 is then replaced by the simpler nζ(1 − n) = −Bn. (See the paper of S. C. Woon.)
(Note that in the foregoing equation for n = 0 and n = 1 the expression −nζ(1 − n) is to be understood as limx → n −xζ(1 − x).)
Applications of the Bernoulli numbers
Asymptotic analysis
Arguably the most important application of the Bernoulli number in mathematics is their use in the Euler–MacLaurin formula. Assuming that ƒ is a sufficiently often differentiable function the Euler–MacLaurin formula can be written as [4]
This formulation assumes the convention B1 = −1/2. However, if one sets B1 = 1/2 then this formula can also be written as
Here ƒ(0) = ƒ which is a commonly used notation identifying the zero-th derivative of ƒ with ƒ. Moreover, let ƒ(−1) denote an antiderivative of ƒ. By the fundamental theorem of calculus,
Thus the last formula can be further simplified to the following succinct form of the Euler–Maclaurin formula
This form is for example the source for the important Euler–MacLaurin expansion of the zeta function (B1 = 1/2)
Here 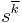 denotes the rising factorial power.[5]
denotes the rising factorial power.[5]
Bernoulli numbers are also frequently used in other kinds of asymptotic expansions. The following example is the classical Poincaré-type asymptotic expansion of the digamma function (again B1 = 1/2).
Use in topology
The Kervaire–Milnor formula for the order of the cyclic group of diffeomorphism classes of exotic (4n − 1)-spheres which bound parallelizable manifolds involves Bernoulli numbers. Let ESn be the number of such exotic spheres for n ≥ 2, then
The Hirzebruch signature theorem for the L genus of a smooth oriented closed manifold of dimension 4n also involves Bernoulli numbers.
Combinatorial definitions
The connection of the Bernoulli number to various kinds of combinatorial numbers is based on the classical theory of finite differences and on the combinatorial interpretation of the Bernoulli numbers as an instance of a fundamental combinatorial principle, the inclusion-exclusion principle.
Connection with Worpitzky numbers
The definition to proceed with was developed by Julius Worpitzky in 1883. Besides elementary arithmetic only the factorial function n! and the power function km is employed. The signless Worpitzky numbers are defined as
They can also be expressed through the Stirling numbers of the second kind
A Bernoulli number is then introduced as an inclusion-exclusion sum of Worpitzky numbers weighted by the sequence 1, 1/2, 1/3,...
This representation has B1 = 1/2.
| Worpitzky's representation of the Bernoulli number | ||
| B0 | = | 1/1 |
| B1 | = | 1/1 − 1/2 |
| B2 | = | 1/1 − 3/2 + 2/3 |
| B3 | = | 1/1 − 7/2 + 12/3 − 6/4 |
| B4 | = | 1/1 − 15/2 + 50/3 − 60/4 + 24/5 |
| B5 | = | 1/1 − 31/2 + 180/3 − 390/4 + 360/5 − 120/6 |
| B6 | = | 1/1 − 63/2 + 602/3 − 2100/4 + 3360/5 − 2520/6 + 720/7 |
A second formula representing the Bernoulli numbers by the Worpitzky numbers is for n ≥ 1
Connection with Stirling numbers of the second kind
A similar combinatorial representation derives from
Here the Bernoulli numbers are an inclusion-exclusion over the set of length-n words, where the sum is taken over all words of length n with k distinct letters, and normalized by k + 1. The combinatorics of this representation can be seen from:
Connection with Stirling numbers of the first kind
The two main formulas relating the unsigned Stirling numbers of the first kind ![\left[\begin{matrix} n \\ m \end{matrix}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/b797e1cd39f8796236f0736f8fa9ca37.png) to the Bernoulli numbers (with B1 = 1/2) are
to the Bernoulli numbers (with B1 = 1/2) are
and the inversion of this sum (for n ≥ 0, m ≥ 0)
Here the number An,m are the rational Akiyama–Tanigawa number, the first few of which are displayed in the following table.
| Akiyama–Tanigawa number | |||||
| n \ m | 0 | 1 | 2 | 3 | 4 |
| 0 | 1 | 1/2 | 1/3 | 1/4 | 1/5 |
| 1 | 1/2 | 1/3 | 1/4 | 1/5 | ... |
| 2 | 1/6 | 1/6 | 3/20 | ... | ... |
| 3 | 0 | 1/30 | ... | ... | ... |
| 4 | −1/30 | ... | ... | ... | ... |
The Akiyama–Tanigawa numbers satisfy a simple recurrence relation which can be exploited to iteratively compute the Bernoulli numbers. This leads to the algorithm shown in the section 'algorithmic description' above.
Connection with Eulerian numbers
There are formulas connecting Eulerian numbers 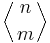 to Bernoulli numbers:
to Bernoulli numbers:
Both formulas are valid for n ≥ 0 if B1 is set to ½. If B1 is set to −½ they are valid only for n ≥ 1 and n ≥ 2 respectively.
A binary tree representation
The Stirling polynomials σn(x) are related to the Bernoulli numbers by Bn = n!σn(1). S. C. Woon (Woon 1997) described an algorithm to compute σn(1) as a binary tree.
| Woon's tree for σn(1) |
Woon's recursive algorithm (for n ≥ 1) starts by assigning to the root node N = [1,2]. Given a node N = [a1,a2,..., ak] of the tree, the left child of the node is L(N) = [−a1,a2 + 1, a3, ..., ak] and the right child R(N) = [a1,2, a2, ..., ak].
Given a node N the factorial of N is defined as
Restricted to the nodes N of a fixed tree-level n the sum of 1/N! is σn(1), thus
For example B1 = 1!(1/2!), B2 = 2!(−1/3! + 1/(2!2!)), B3 = 3!(1/4! − 1/(2!3!) − 1/(3!2!) + 1/(2!2!2!)).
Asymptotic approximation
Leonhard Euler expressed the Bernoulli numbers in terms of the Riemann zeta function as
It then follows from the Stirling formula that, as n goes to infinity,
Including more terms from the zeta series yields a better approximation, as does factoring in the asymptotic series in Stirling's approximation.
Integral representation and continuation
The integral
has as special values b(2n) = B2n for n > 0. The integral might be considered as a continuation of the Bernoulli numbers to the complex plane and this was indeed suggested by Peter Luschny in 2004.
For example b(3) = (3/2)ζ(3)Π−3Ι and b(5) = −(15/2) ζ(5) Π −5Ι. Here ζ(n) denotes the Riemann zeta function and Ι the imaginary unit. It is remarkable that already Leonhard Euler (Opera Omnia, Ser. 1, Vol. 10, p. 351) considered these numbers and calculated
Euler's values are unsigned and real, but obviously his aim was to find a meaningful way to define the Bernoulli numbers at the odd integers n > 1.
The relation to the Euler numbers and π
The Euler numbers are a sequence of integers intimately connected with the Bernoulli numbers. Comparing the asymptotic expansions of the Bernoulli and the Euler numbers shows that the Euler numbers E2n are in magnitude approximately (2/π)(42n − 22n) times larger than the Bernoulli numbers B2n. In consequence:
This asymptotic equation reveals that π lies in the common root of both the Bernoulli and the Euler numbers. In fact π could be computed from these rational approximations.
Bernoulli numbers can be expressed through the Euler numbers and vice versa. Since for n odd Bn = En = 0 (with the exception B1), it suffices to consider the case when n is even.
These conversion formulas express an inverse relation between the Bernoulli and the Euler numbers. But more important, there is a deep arithmetic root common to both kinds of numbers, which can be expressed through a more fundamental sequence of numbers, also closely tied to π. These numbers are defined for n > 1 as
and S1 = 1 by convention (Elkies 2003). The magic of these numbers lies in the fact that they turn out to be rational numbers. This was first proved by Leonhard Euler in a landmark paper (Euler 1735) ‘De summis serierum reciprocarum’ (On the sums of series of reciprocals) and has fascinated mathematicians ever since. The first few of these numbers are
The Bernoulli numbers and Euler numbers are best understood as special views of these numbers, selected from the sequence Sn and scaled for use in special applications.
The expression [n even] has the value 1 if n is even and 0 otherwise (Iverson bracket).
These identities show that the quotient of Bernoulli and Euler numbers at the beginning of this section is just the special case of Rn = 2Sn / Sn+1 when n is even. The Rn are rational approximations to π and two successive terms always enclose the true value of π. Beginning with n = 1 the sequence starts
These rational numbers also appear in the last paragraph of Euler's paper cited above.
An algorithmic view: the Seidel triangle
The sequence Sn has another unexpected yet important property: The denominators of Sn divide the factorial (n − 1)!. In other words: the numbers Tn = Sn(n − 1)! are integers.
Thus the above representations of the Bernoulli and Euler numbers can be rewritten in terms of this sequence as
These identities make it easy to compute the Bernoulli and Euler numbers: the Euler numbers En are given immediately by T2n + 1 and the Bernoulli numbers B2n are obtained from T2n by some easy shifting, avoiding rational arithmetic.
What remains is to find a convenient way to compute the numbers Tn. However, already in 1877 Philipp Ludwig von Seidel (Seidel 1877) published an ingenious algorithm which makes it extremely simple to calculate Tn.
| Seidel's algorithm for Tn |
[begin] Start by putting 1 in row 0 and let k denote the number of the row currently being filled. If k is odd, then put the number on the left end of the row k − 1 in the first position of the row k, and fill the row from the left to the right, with every entry being the sum of the number to the left and the number to the upper. At the end of the row duplicate the last number. If k is even, proceed similar in the other direction. [end]
Seidel's algorithm is in fact much more general (see the exposition of Dominique Dumont (Dumont 1981)) and was rediscovered several times thereafter.
Similar to Seidel's approach D. E. Knuth and T. J. Buckholtz (Knuth & Buckholtz 1967) gave a recurrence equation for the numbers T2n and recommended this method for computing B2n and E2n ‘on electronic computers using only simple operations on integers’.
V. I. Arnold rediscovered Seidel's algorithm in (Arnold 1991) and later Millar, Sloane and Young popularized Seidel's algorithm under the name boustrophedon transform.
A combinatorial view: alternating permutations
Around 1880, three years after the publication of Seidel's algorithm, Désiré André proved a now classic result of combinatorial analysis (André 1879) & (André 1881). Looking at the first terms of the Taylor expansion of the trigonometric functions tan x and sec x André made a startling discovery.
The coefficients are the Euler numbers of odd and even index, respectively. In consequence the ordinary expansion of tan x + sec x has as coefficients the rational numbers Sn.
André then succeeded by means of a recurrence argument to show that the alternating permutations of odd size are enumerated by the Euler numbers of odd index (also called tangent numbers) and the alternating permutations of even size by the Euler numbers of even index (also called secant numbers).
Generalizations by polynomials
The Bernoulli polynomials can be regarded as generalizations of the Bernoulli numbers the same as the Euler polynomials are generalizations of the Euler numbers.
Arithmetical properties of the Bernoulli numbers
The Bernoulli numbers can be expressed in terms of the Riemann zeta function as Bn = − nζ(1 − n) for integers n ≥ 0 provided for n = 0 and n = 1 the expression − nζ(1 − n) is understood as the limiting value and the convention B1 = 1/2 is used. This intimately relates them to the values of the zeta function at negative integers. As such, they could be expected to have and do have deep arithmetical properties. For example, the Agoh–Giuga conjecture postulates that p is a prime number if and only if pBp−1 is congruent to −1 modulo p. Divisibility properties of the Bernoulli numbers are related to the ideal class groups of cyclotomic fields by a theorem of Kummer and its strengthening in the Herbrand-Ribet theorem, and to class numbers of real quadratic fields by Ankeny–Artin–Chowla.
The Kummer theorems
The Bernoulli numbers are related to Fermat's last theorem (FLT) by Kummer's theorem (Kummer 1850), which says:
If the odd prime p does not divide any of the numerators of the Bernoulli numbers B2, B4, ..., Bp−3 then xp + yp + zp = 0 has no solutions in non-zero integers.
Prime numbers with this property are called regular primes. Another classical result of Kummer (Kummer 1851) are the following congruences.
Let p be an odd prime and b an even number such that p − 1 does not divide b. Then for any non-negative integer k
A generalization of these congruences goes by the name of p-adic continuity.
p-adic continuity
If b, m and n are positive integers such that m and n are not divisible by p − 1 and 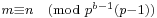 , then
, then
Since Bn = —n ζ(1 — n), this can also be written
where u = 1 − m and v = 1 − n, so that u and v are nonpositive and not congruent to 1 modulo p − 1. This tells us that the Riemann zeta function, with 1 − p−s taken out of the Euler product formula, is continuous in the p-adic numbers on odd negative integers congruent modulo p − 1 to a particular 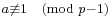 , and so can be extended to a continuous function ζp(s) for all p-adic integers
, and so can be extended to a continuous function ζp(s) for all p-adic integers 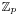 , the p-adic zeta function.
, the p-adic zeta function.
Ramanujan's congruences
The following relations, due to Ramanujan, provide a more efficient method for calculating Bernoulli numbers:
Von Staudt–Clausen theorem
The von Staudt–Clausen theorem was given by Karl Georg Christian von Staudt (von Staudt 1840) and Thomas Clausen (Clausen 1840) independently in 1840. The theorem affirms the existence of a number In. which is either an integer or 1⁄2, such that
The sum is over the primes p for which p − 1 divides n. These are the same primes which are employed in the Clausen algorithm. The proposition holds true for all n > 0, not only for even n. I1 = 1 and for odd n > 1, In = 1⁄2 (and I2n is always an integer).
A consequence of the von Staudt–Clausen theorem is: the denominators of the Bernoulli numbers are square-free and for n ≥ 2 divisible by 6.
Why do the odd Bernoulli numbers vanish?
The sum
can be evaluated for negative values of the index n. Doing so will show that it is an odd function for even values of k, which implies that the sum has only terms of odd index. This and the formula for the Bernoulli sum imply that B2k+1−m is 0 for m odd and greater than 1; and that the term for B1 is cancelled by the subtraction. The von Staudt Clausen theorem combined with Worpitzky's representation also gives a combinatorial answer to this question (valid for n > 1).
From the von Staudt Clausen theorem it is known that for odd n > 1 the number 2Bn is an integer. This seems trivial if one knows beforehand that in this case Bn = 0. However, by applying Worpitzky's representation one gets
as a sum of integers, which is not trivial. Here a combinatorial fact comes to surface which explains the vanishing of the Bernoulli numbers at odd index. Let Sn,m be the number of surjective maps from {1, 2, ..., n} to {1, 2, ..., m}, then 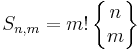 . The last equation can only hold if
. The last equation can only hold if
This equation can be proved by induction. The first two examples of this equation are
- n = 4: 2 + 8 = 7 + 3,
- n = 6: 2 + 120 + 144 = 31 + 195 + 40.
Thus the Bernoulli numbers vanish at odd index because some non-obvious combinatorial identities are embodied in the Bernoulli numbers.
A restatement of the Riemann hypothesis
The connection between the Bernoulli numbers and the Riemann zeta function is strong enough to provide an alternate formulation of the Riemann hypothesis (RH) which uses only the Bernoulli number. In fact Marcel Riesz (Riesz 1916) proved that the RH is equivalent to the following assertion:
For every ε > 1/4 there exists a constant Cε > 0 (depending on ε) such that |R(x)| < Cε xε as x → ∞.
Here R(x) is the Riesz function
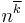 denotes the rising factorial power in the notation of D. E. Knuth. The number βn = Bn/n occur frequently in the study of the zeta function and are significant because βn is a p-integer for primes p where p − 1 does not divide n. The βn are called divided Bernoulli number.
denotes the rising factorial power in the notation of D. E. Knuth. The number βn = Bn/n occur frequently in the study of the zeta function and are significant because βn is a p-integer for primes p where p − 1 does not divide n. The βn are called divided Bernoulli number.
History
Early history
The Bernoulli numbers are rooted in the early history of the computation of sums of integer powers, which have been of interest to mathematicians since antiquity.
Methods to calculate the sum of the first n positive integers, the sum of the squares and of the cubes of the first n positive integers were known, but there were no real 'formulas', only descriptions given entirely in words. Among the great mathematicians of antiquity which considered this problem were: Pythagoras (c. 572–497 BCE, Greece), Archimedes (287–212 BCE, Italy), Aryabhata (b. 476, India), Abu Bakr al-Karaji (d. 1019, Persia) and Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham (965–1039, Egypt).
During the late sixteenth and early seventeenth centuries mathematicians made significant progress. In the West Thomas Harriot (1560–1621) of England, Johann Faulhaber (1580–1635) of Germany, Pierre de Fermat (1601–1665) and fellow French mathematician Blaise Pascal (1623–1662) all played important roles.
Thomas Harriot seems to have been the first to derive and write formulas for sums of powers using symbolic notation, but even he calculated only up to the sum of the fourth powers. Johann Faulhaber gave formulas for sums of powers up to the 17th power in his 1631 Academia Algebrae, far higher than anyone before him, but he did not give a general formula.
The Swiss mathematician Jakob Bernoulli (1654–1705) was the first to realize the existence of a single sequence of constants B0, B1, B2, ... which provide a uniform formula for all sums of powers (Knuth 1993).
The joy Bernoulli experienced when he hit upon the pattern needed to compute quickly and easily the coefficients of his formula for the sum of the c-th powers for any positive integer c can be seen from his comment. He wrote:
“With the help of this table, it took me less than half of a quarter of an hour to find that the tenth powers of the first 1000 numbers being added together will yield the sum
91,409,924,241,424,243,424,241,924,242,500.”
Bernoulli's result was published posthumously in Ars Conjectandi in 1713. Seki Kōwa independently discovered the Bernoulli numbers and his result was published a year earlier, also posthumously, in 1712.[1] However, Seki did not present his method as a formula based on a sequence of constants.
Bernoulli's formula for sums of powers is the most useful and generalizable formulation to date. The coefficients in Bernoulli's formula are now called Bernoulli numbers, following a suggestion of Abraham de Moivre.
Bernoulli's formula is sometimes called Faulhaber's formula after Johann Faulhaber who found remarkable ways to calculate sum of powers but never stated Bernoulli's formula. To call Bernoulli's formula Faulhaber's formula does injustice to Bernoulli and simultaneously hides the genius of Faulhaber as Faulhaber's formula is in fact more efficient than Bernoulli's formula. According to Knuth (Knuth 1993) a rigorous proof of Faulhaber’s formula was first published by Carl Jacobi in 1834 (Jacobi 1834). Donald E. Knuth's in-depth study of Faulhaber's formula concludes:
“Faulhaber never discovered the Bernoulli numbers; i.e., he never realized that a single sequence of constants B0, B1, B2, ... would provide a uniform
for all sums of powers. He never mentioned, for example, the fact that almost half of the coefficients turned out to be zero after he had converted his formulas for 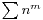 from polynomials in N to polynomials in n.” (Knuth 1993, p. 14)
from polynomials in N to polynomials in n.” (Knuth 1993, p. 14)
Reconstruction of 'Summae Potestatum'
The Bernoulli numbers were introduced by Jakob Bernoulli in the book Ars Conjectandi published posthumously in 1713. The main formula can be seen in the second half of the corresponding facsimile. The constant coefficients denoted A, B, C and D by Bernoulli are mapped to the notation which is now prevalent as A = B2, B = B4, C = B6, D = B8. In the expression c·c−1·c−2·c−3 the small dots are used as grouping symbols, not as signs for multiplication. Using today's terminology these expressions are falling factorial powers 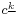 . The factorial notation k! as a shortcut for 1 × 2 × ... × k was not introduced until 100 years later. The integral symbol on the left hand side goes back to Gottfried Wilhelm Leibniz in 1675 who used it as a long letter S for "summa" (sum). (The Mathematics Genealogy Project [6] shows Leibniz as the doctoral adviser of Jakob Bernoulli. See also the Earliest Uses of Symbols of Calculus.[7]) The letter n on the left hand side is not an index of summation but gives the upper limit of the range of summation which is to be understood as 1, 2, …, n. Putting things together, for positive c, today a mathematician is likely to write Bernoulli's formula as:
. The factorial notation k! as a shortcut for 1 × 2 × ... × k was not introduced until 100 years later. The integral symbol on the left hand side goes back to Gottfried Wilhelm Leibniz in 1675 who used it as a long letter S for "summa" (sum). (The Mathematics Genealogy Project [6] shows Leibniz as the doctoral adviser of Jakob Bernoulli. See also the Earliest Uses of Symbols of Calculus.[7]) The letter n on the left hand side is not an index of summation but gives the upper limit of the range of summation which is to be understood as 1, 2, …, n. Putting things together, for positive c, today a mathematician is likely to write Bernoulli's formula as:
In fact this formula imperatively suggests to set B1 = ½ when switching from the so-called 'archaic' enumeration which uses only the even indices 2, 4, … to the modern form (more on different conventions in the next paragraph). Most striking in this context is the fact that the falling factorial 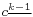 has for k = 0 the value
has for k = 0 the value 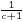 .[8] Thus Bernoulli's formula can and has to be written:
.[8] Thus Bernoulli's formula can and has to be written:
If B1 stands for the value Bernoulli himself has given to the coefficient at that position.
Generalized Bernoulli numbers
The generalized Bernoulli numbers are certain algebraic numbers, defined similarly to the Bernoulli numbers, that are related to special values of Dirichlet L-functions in the same way that Bernoulli numbers are related to special values of the Riemann zeta function.
Let χ be a primitive Dirichlet character modulo f. The generalized Bernoulli numbers attached to χ are defined by
Let ε ∈ {0, 1} be defined by χ(−1) = (−1)ε. Then,
- Bk,χ ≠ 0 if, and only if, k ≡ ε (mod 2).
Generalizing the relation between Bernoulli numbers and values of the Riemann zeta function at non-positive integers, one has the for all integers k ≥ 1
where L(s, χ) is the Dirichlet L-function of χ.[9]
Appendix
Assorted identities
- A compact form of Bernoulli's formula makes use of an abstract symbol B:
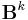 that appears during binomial expansion of the parenthesized term is to be replaced by the Bernoulli number
that appears during binomial expansion of the parenthesized term is to be replaced by the Bernoulli number 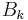 (and
(and 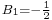 ). More suggestively and mnemonically, this may be written as a definite integral:
). More suggestively and mnemonically, this may be written as a definite integral:
- Let n be non-negative and even
- The nth cumulant of the uniform probability distribution on the interval [−1, 0] is Bn/n.
- Let n¡ = 1/n! and n ≥ 1. Then Bn is the following determinant:
Bn = 1
───
n¡2¡ 1¡ 0 0 0 ... 0 3¡ 2¡ 1¡ 0 0 ... 0 4¡ 3¡ 2¡ 1¡ 0 ... 0 ... ... ... ... ... ... ... (n − 1)¡ ... ... 3¡ 2¡ 1¡ 0 n¡ (n − 1)¡ ... ... 3¡ 2¡ 1¡ (n + 1)¡ n¡ (n − 1)¡ ... ... 3¡ 2¡ Thus the determinant is σn(1), the Stirling polynomial at x = 1.
- For even-numbered Bernoulli numbers, B2p is given by the p X p determinant:[10]
B2p = (−1)p+1
───
(22p − 2)(2p)¡3¡ 1¡ 0 0 0 ... 0 5¡ 3¡ 1¡ 0 0 ... 0 7¡ 5¡ 3¡ 1¡ 0 ... 0 ... ... ... ... ... ... ... (2p − 3)¡ ... ... 5¡ 3¡ 1¡ 0 (2p − 1)¡ (2p − 3)¡ ... ... 5¡ 3¡ 1¡ (2p + 1)¡ (2p − 1)¡ (2p − 3)¡ ... ... 5¡ 3¡ - Let n ≥ 1.
- Let n ≥ 1. Then (von Ettingshausen 1827)
- Let n ≥ 0. Then (Leopold Kronecker 1883)
- Let n ≥ 1 and m ≥ 1. Then (Carlitz 1968)
-
Let n ≥ 4 and
the harmonic number. Then
-
Let n ≥ 4. Yuri Matiyasevich found (1997)
-
Let n ≥ 1
This is an identity by Faber-Pandharipande-Zagier-Gessel. Choose x = 0 or x = 1 to get a Bernoulli number identity according to your favourite convention.
- The next formula is true for n ≥ 0 if B1 = B1(1) = 1/2, but only for n ≥ 1 if B1 = B1(0) = −1/2.
- Let n ≥ 0 and [b] = 1 if b is true, 0 otherwise.
Values of the Bernoulli numbers
Bn = 0 for all odd n other than 1. The first few non-zero Bernoulli numbers are:
| n | Numerator | Denominator | Decimal approximation |
|---|---|---|---|
| 0 | 1 | 1 | +1.00000000000 |
| 1 | −1 | 2 | −0.50000000000 |
| 2 | 1 | 6 | +0.16666666667 |
| 4 | −1 | 30 | −0.03333333333 |
| 6 | 1 | 42 | +0.02380952381 |
| 8 | −1 | 30 | −0.03333333333 |
| 10 | 5 | 66 | +0.07575757576 |
| 12 | −691 | 2730 | −0.25311355311 |
| 14 | 7 | 6 | +1.16666666667 |
| 16 | −3617 | 510 | −7.09215686275 |
| 18 | 43867 | 798 | +54.9711779448 |
| OEIS | A027641 | A027642 |
See also
- Kummer's congruences
- poly-Bernoulli number
- Bernoulli polynomials
- Riemann zeta function
- Hurwitz zeta function
- Euler number
- Euler summation
Notes
- ^ a b Selin, H. (1997), p. 891
- ^ Smith, D. E. (1914), p. 108
- ^ Note G in the Menabrea reference
- ^ Concrete Mathematics, (9.67).
- ^ Concrete Mathematics, (2.44) and (2.52)
- ^ Mathematics Genealogy Project
- ^ Earliest Uses of Symbols of Calculus
- ^ Graham, R.; Knuth, D. E.; Patashnik, O. (1989), Concrete Mathematics (2nd ed.), Addison-Wesley, Section 2.51, ISBN 0-201-55802-5
- ^ Neukirch 1999, §VII.2
- ^ Jerome Malenfant (2011). "Finite, closed-form expressions for the partition function and for Euler, Bernoulli, and Stirling numbers". arXiv:1103.1585 [math.NT].
References
- Abramowitz, M.; Stegun, C. A. (1972), "§23.1: Bernoulli and Euler Polynomials and the Euler-Maclaurin Formula", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (9th printing ed.), New York: Dover, pp. 804–806.
- André, D. (1879), "Développements de sec x et tan x", Comptes Rendus Acad. Sci. 88: 965–967.
- André, D. (1881), "Mémoire sur les permutations alternées", J. Math. 7: 167–184.
- Arlettaz, D. (1998), "Die Bernoulli-Zahlen: eine Beziehung zwischen Topologie und Gruppentheorie", Math. Semesterber 45: 61–75, doi:10.1007/s005910050037.
- Arnold, V. I. (1991), "Bernoulli-Euler updown numbers associated with function singularities, their combinatorics and arithmetics", Duke Math. J. 63: 537–555.
- Ayoub, A.; Lee, F. W.; Anderson, J. A.; Vicharelli, P. A.; Popescu, D.; Popescu, Iovitzu (1981), "Euler and the Zeta Function", Amer. Math. Monthly 74 (2): 1067–1086.
- Buhler, J.; Crandall, R.; Ernvall, R.; Metsankyla, T.; Shokrollahi, M. (2001), "Irregular Primes and Cyclotomic Invariants to 12 Million", Journal of Symbolic Computation 31 (1–2): 89–96, doi:10.1006/jsco.1999.1011.
- Carlitz, L. (1968), "Bernoulli Numbers", Fib. Quart. 6: 71–85.
- Clausen, Thomas (1840), "Lehrsatz aus einer Abhandlung über die Bernoullischen Zahlen", Astr. Nachr. 17 (22): 351–352, doi:10.1002/asna.18400172205.
- Conway, John; Guy (1996), The Book of Numbers, Springer-Verlag.
- Dilcher, K.; Skula, L.; Slavutskii, I. Sh. (1991), "Bernoulli numbers. Bibliography (1713–1990)", Queen's Papers in Pure and Applied Mathematics (Kingston, Ontario) (87), http://www.mscs.dal.ca/~dilcher/bernoulli.html.
- Dumont, D.; Viennot, G. (1980), "A combinatorial interpretation of Seidel generation of Genocchi numbers", Ann. Discrete Math., Annals of Discrete Mathematics 6: 77–87, doi:10.1016/S0167-5060(08)70696-4, ISBN 9780444860484.
- Dumont, D. (1981), "Matrices d'Euler-Seidel", Séminaire Lotharingien de Combinatoire, http://emis.u-strasbg.fr/journals/SLC/opapers/s05dumont.html.
- Elkies, N. D. (2003), "On the sums Sum_(k=-infinity...infinity) (4k+1)^(-n)", Amer. Math. Monthly 110 (7): 561–573, arXiv:math.CA/0101168
- Entringer, R. C. (1966), "A combinatorial interpretation of the Euler and Bernoulli numbers", Nieuw. Arch. V. Wiskunde 14: 241–6.
- von Ettingshausen, A. (1827), Vorlesungen über die höhere Mathematik, Bd. 1, Vienna: Carl Gerold.
- Euler, Leonhard (1735), "De summis serierum reciprocarum", Opera Omnia I.14, E 41,: 73–86, arXiv:math/0506415
- Fee, G.; Plouffe, S. (2007), "An efficient algorithm for the computation of Bernoulli numbers", Eprint arXiv:math/0702300, arXiv:math/0702300.
- Gould, Henry W. (1972), "Explicit formulas for Bernoulli numbers", Amer. Math. Monthly 79: 44–51
- Graham, R. L.; Knuth, D. E.; Patashnik, O. (1989), Concrete Mathematics, Addison-Wesley.
- Guo, Victor J. W.; Zeng, Jiang (2005), "A q-Analogue of Faulhaber's Formula for Sums of Powers", The Electronic Journal of Combinatorics 11 (2): 1441, arXiv:math/0501441, Bibcode 2005math......1441G, http://www.combinatorics.org/Volume_11/Abstracts/v11i2r19.html.
- Harvey, David (2010), "A multimodular algorithm for computing Bernoulli numbers", Math. Comput. 79 (272): 2361–2370, arXiv:0807.1347, doi:10.1090/S0025-5718-2010-02367-1, Zbl 05797914.
- Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory, Springer-Verlag.
- Jacobi, C. G. J. (1834), "De usu legitimo formulae summatoriae Maclaurinianae", Journal für die reine und angewandte Mathematik 12: 263–272.
- Jordan, Charles (1950), Calculus of Finite Differences, New York: Chelsea Publ. Co..
- Kaneko, M. (2000), "The Akiyama-Tanigawa algorithm for Bernoulli numbers", Journal of Integer Sequences 12: 29, Bibcode 2000JIntS...3...29K, http://www.cs.uwaterloo.ca/journals/JIS/vol3.html.
- Kellner, Bernd (2002), Program Calcbn – A program for calculating Bernoulli numbers, http://www.bernoulli.org/.
- Knuth, D. E.; Buckholtz, T. J. (1967), "Computation of Tangent, Euler, and Bernoulli Numbers", Mathematics of Computation (American Mathematical Society) 21 (100): 663–688, doi:10.2307/2005010, JSTOR 2005010.
- Knuth, D. E. (1993), "Johann Faulhaber and the Sums of Powers", Mathematics of Computation (American Mathematical Society) 61 (203): 277–294, arXiv:math/9207222, doi:10.2307/2152953, JSTOR 2152953.
- Kummer, E. E. (1850), "Allgemeiner Beweis des Fermat'schen Satzes, dass die Gleichung xλ + yλ = zλ durch ganze Zahlen unlösbar ist, für alle diejenigen Potenz-Exponenten λ, welche ungerade Primzahlen sind und in den Zählern der ersten (λ-3)/2 Bernoulli'schen Zahlen als Factoren nicht vorkommen", J. Reine Angew. Math. 40: 131–138, http://www.digizeitschriften.de/resolveppn/GDZPPN002146738.
- Kummer, E. E. (1851), "Über eine allgemeine Eigenschaft der rationalen Entwicklungscoefficienten einer bestimmten Gattung analytischer Functionen", J. Reine Angew. Math. 41: 368–372, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002147319.
- Luschny, Peter (2007), An inclusion of the Bernoulli numbers, http://www.luschny.de/math/primes/bernincl.html.
- Menabrea, L. F. (1842), "Sketch of the Analytic Engine invented by Charles Babbage, with notes upon the Memoir by the Translator Ada Augusta, Countess of Lovelace", Bibliothèque Universelle de Genève 82, http://www.fourmilab.ch/babbage/sketch.html
- Milnor, John W.; Stasheff, James D. (1974), "Appendix B: Bernoulli Numbers", Characteristic Classes, Annals of Mathematics Studies, 76, Princeton University Press and University of Tokyo Press, pp. 281–287.
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, MR1697859
- Pavlyk, Oleksandr (2008), Today We Broke the Bernoulli Record: From the Analytical Engine to Mathematica, Wolfram Blog, http://blog.wolfram.com/2008/04/29/today-we-broke-the-bernoulli-record-from-the-analytical-engine-to-mathematica/.
- Riesz, M. (1916), "Sur l'hypothèse de Riemann", Acta Mathematica 40: 185–90, doi:10.1007/BF02418544.
- Saalschütz, Louis (1893), Vorlesungen über die Bernoullischen Zahlen, ihren Zusammenhang mit den Secanten-Coefficienten und ihre wichtigeren Anwendungen, Berlin: Julius Springer, http://digital.library.cornell.edu/cgi/t/text/text-idx?c=math;idno=00450002.
- Seidel, L. (1877), "Über eine einfache Entstehungsweise der Bernoullischen Zahlen und einiger verwandten Reihen", Sitzungsber. Münch. Akad. 4: 157–187.
- Selin, Helaine (1997), "Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures", Encyclopaedia of the History of Science (Springer): 819, Bibcode 2008ehst.book.....S, ISBN 0792340663.
- Slavutskii, Ilya Sh. (1995), "Staudt and arithmetical properties of Bernoulli numbers", Historia Scientiarum 2: 69–74.
- Smith, David Eugene; Mikami, Yoshio (1914), A history of Japanese mathematics, Open Court publishing company, ISBN 9780486434827, http://books.google.com/?id=pTcQsvfbSu4C&pg=PA108.
- von Staudt, K. G. Ch. (1840), "Beweis eines Lehrsatzes, die Bernoullischen Zahlen betreffend", Journal für die reine und angewandte Mathematik 21: 372–374.
- von Staudt, K. G. Ch. (1845), "De numeris Bernoullianis, commentationem alteram", Erlangen.
- Sun, Zhi-Wei (2005/2006), Some curious results on Bernoulli and Euler polynomials, http://pweb.nju.edu.cn/zwsun.
- Woon, S. C. (1997), "A tree for generating Bernoulli numbers", Math. Mag. 70 (1): 51–56, doi:10.2307/2691054, JSTOR 2691054.
- Woon, S. C. (1998). "Generalization of a relation between the Riemann zeta function and Bernoulli numbers". arXiv:math.NT/9812143 [math.NT]..
- Worpitzky, J. (1883), "Studien über die Bernoullischen und Eulerschen Zahlen", Journal für die reine und angewandte Mathematik 94: 203–232, http://resolver.sub.uni-goettingen.de/purl?GDZPPN002158698.
External links
- The first 498 Bernoulli Numbers from Project Gutenberg
- The first 10,000 Bernoulli numbers
- A multimodular algorithm for computing Bernoulli numbers
- The Bernoulli Number Page
- Bernoulli number programs at LiteratePrograms
- Weisstein, Eric W., "Bernoulli Number" from MathWorld.
- The Computation of Irregular Primes
- Bernoullinumbers in context of Pascal-(Binomial)matrix german version
- summing of like powers in context with Pascal-/Bernoulli-matrix
- Some special properties, sums of Bernoulli-and related numbers
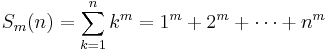
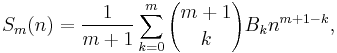
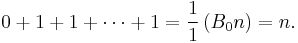
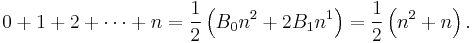
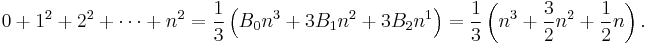
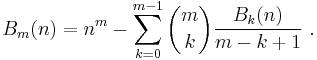
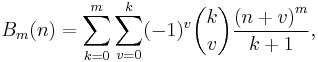
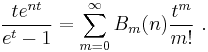
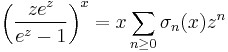

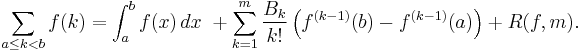
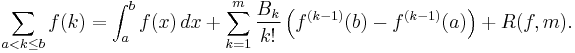
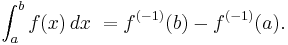
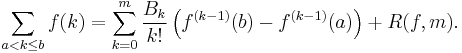
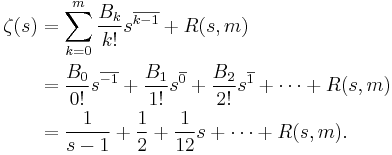
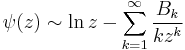
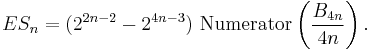
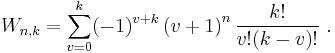
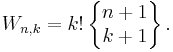
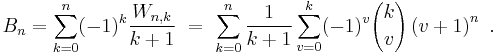
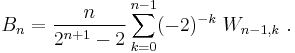
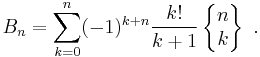
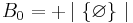

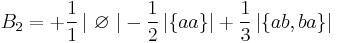
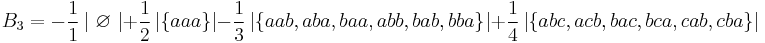
![\frac{1}{m!}\sum_{k=0}^m (-1)^{k} \left[\begin{matrix} m%2B1 \\ k%2B1 \end{matrix}\right] B_k = \frac{1}{m%2B1},](/2012-wikipedia_en_all_nopic_01_2012/I/5ebafb764b44b888ce26962fca67743a.png)
![\frac{1}{m!}\sum_{k=0}^m (-1)^{k} \left[\begin{matrix} m%2B1 \\ k%2B1 \end{matrix}\right] B_{n%2Bk} = A_{n,m}.](/2012-wikipedia_en_all_nopic_01_2012/I/3b52cca332b2652c9b33d472e28e1d5c.png)
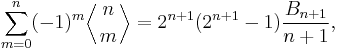
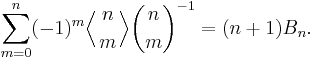
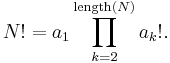
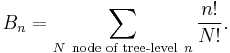
![B_{2n} = (-1)^{n%2B1}\frac {2(2n)!} {(2\pi)^{2n}} \left[1%2B\frac{1}{2^{2n}}%2B\frac{1}{3^{2n}}%2B\frac{1}{4^{2n}}%2B\cdots\;\right].](/2012-wikipedia_en_all_nopic_01_2012/I/d5d80e593f500cf0716e86d76467e89a.png)
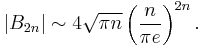
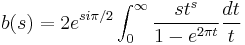
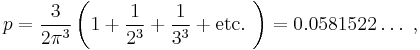
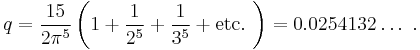
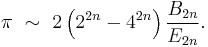
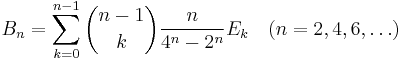
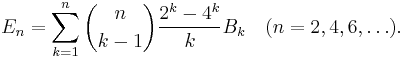
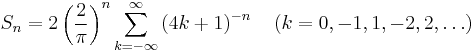
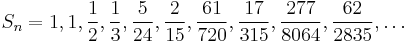
![B_{n} =(-1)^{\left\lfloor n/2\right\rfloor }\left[ n\ \operatorname{even}\right] \frac{n! }{2^n-4^n}\, S_{n}\ , \quad (n=2,3,\ldots) \ ,](/2012-wikipedia_en_all_nopic_01_2012/I/8d5d7d5f31c7c143d5dba018b3b82b40.png)
![E_{n} =(-1)^{\left\lfloor n/2\right\rfloor }\left[ n\ \operatorname{even}\right] n! \, S_{n%2B1} \quad\qquad (n=0,1,\ldots).](/2012-wikipedia_en_all_nopic_01_2012/I/45cfceccf06751f4a470a280ed3b991b.png)
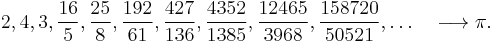
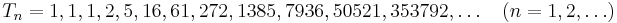
![B_{n} =(-1)^{\left\lfloor n/2\right\rfloor }\left[ n\text{ even}\right] \frac{n }{2^n-4^n}\, T_{n}\ , \quad (n=2,3,\ldots) \ ,](/2012-wikipedia_en_all_nopic_01_2012/I/11bd6b0d5763263bb24ba0f08bf179c8.png)
![E_{n} =(-1)^{\left\lfloor n/2\right\rfloor }\left[ n\text{ even}\right] T_{n%2B1} \quad\quad\qquad(n=0,1,\ldots) \ .](/2012-wikipedia_en_all_nopic_01_2012/I/348e132e247d070686c04817255cf181.png)
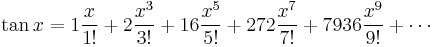
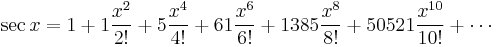
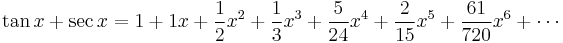
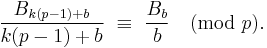
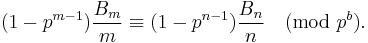
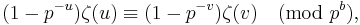
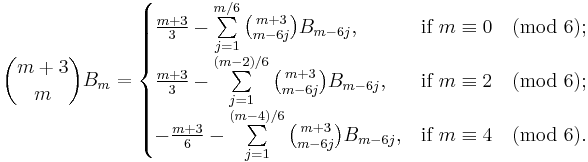
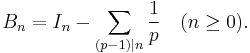
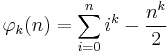
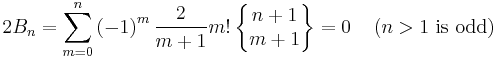
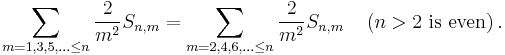
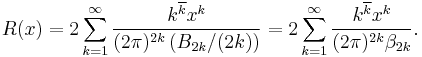
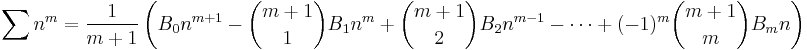
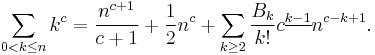
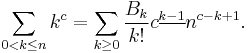
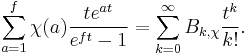
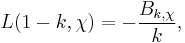
![S_m(n) = {1\over{m%2B1}} [(\mathbf{B} %2B n)^{m%2B1} - B_{m%2B1}]](/2012-wikipedia_en_all_nopic_01_2012/I/1eb1dd3af59f7d6f4b80bba429e62c4e.png)
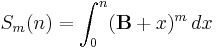
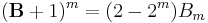
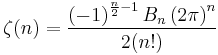
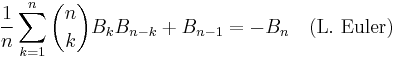
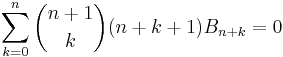
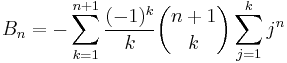
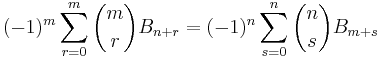
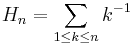
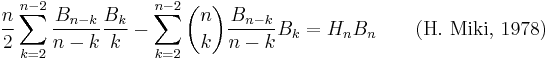
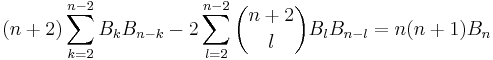
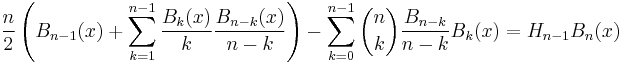
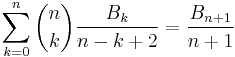
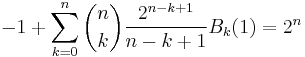
![-1 %2B \sum_{k=0}^n \binom{n}{k} \frac{2^{n-k%2B1}}{n-k%2B1}B_{k}(0) = [n=0]](/2012-wikipedia_en_all_nopic_01_2012/I/eea4ba6f4359d6249b0468749f626739.png)